Collatz-like behavior of Busy Beavers
Nick Drozd just announced a new 4x2 Beeping Busy Beaver champion (BBB(4, 2)). This is a 4-state, 2-symbol Turing Machine which runs for 32,779,478 steps only to produce a blank tape and then run off to left forever in state C. As far as I can tell, the previous record for BBB(4, 2) was 66,349, so this is quite an improvement!
This machine is also a textbook example of Collatz-like behavior, which Pascal Michel has shown to be quite common in BB champions and candidates. I love this sort of analysis so much because it takes these opaque Turing Machines and expresses what they are doing in a simple structured way and shows how these BB candidates are taking advantage of the machinery of an open problem in mathematics (and a little luck) to run for extremely long runtimes.
The Machine
This Turing Machine is defined by the transition table:
| 0 | 1 | |
|---|---|---|
| A | 1RB | 1LD |
| B | 1RC | 1RB |
| C | 1LC | 1LA |
| D | 0RC | 0RD |
Or 1RB1LD_1RC1RB_1LC1LA_0RC0RD in the Standard Text format.
You can see how it performs in an online simulator or using my Visual_Simulator which looks like:
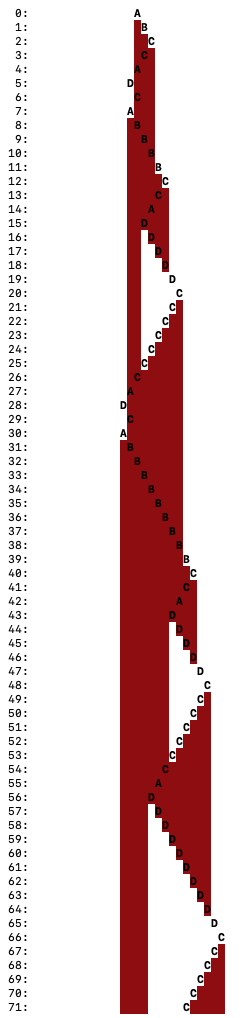
Here, each line is the tape at the step number specified at left. The upper-case letter is the current state and head position. Red means 1 on the tape, White means 0.
Tape Compression
From either of those simulations we can see that it’s performing a sort of two-stage process, moving back and forth from the right side to the middle repeatedly, each iteration moving that middle point towards the left and eventually when it reaches the left resetting in some way and starting over again. This pattern is pretty common among Busy Beaver candidates.
The direct simulations above are great for observing behavior, but become a bit tedious when trying to analyze that behavior. Instead, we often find it useful to use run-length encoding on the tape (I first learned about this technique from Heiner Marxen’s excellent article about Macro Machines). Consider the last line in the image above (Visual_Simulator output at step 71). If we were to write that configuration out in text we could write it as:
... 0 1 1 1 1 0 0 0 0 0 (C0) 1 1 1 1 1 0 ...
In other words, the TM is in state C, reading head over a 0. To the right are 5 1s and then infinitely many 0s. To the left are 5 0s, then 4 1s, then infinitely many 0s. Inspired by this English language description, we can write the tape in such a compressed format:
0∞ 14 05 (C0) 15 0∞
We will use a slight modification of this format:
0∞ 14 06 <C 15 0∞
The difference here being that we represent the TM head as moving towards the 6 0s rather than on top of one of them with 5 to the left.
Chain Step
Now that we are using this tape compression technique let’s see what it looks like if we continue our simulation starting at step 71 (from above):
71: 0∞ 14 06 <C 15 0∞
72: 0∞ 14 05 <C 16 0∞
73: 0∞ 14 04 <C 17 0∞
74: 0∞ 14 03 <C 18 0∞
Can you see a pattern here? Because we have the transition rule C0 → 1LC, we can see that: 0n <C → <C 1n for any n. In other words, when the Turing Machine is in state C, traveling left into a block of 0s, it will travel straight through, converting them all to 1s and continuing on in state C to the left of that block. This is our first Turing Machine simulation acceleration technique! I call this a chain step, because it allows us to jump over entire “chains” of symbols.
Rule Step
Now with tape compression and chain steps, we are equipped to see some higher-level patterns.
Now with this new representation we can see some patterns more easily. Jumping ahead a bit to step 138:
138: 0∞ 116 05 C> 0∞
139: 0∞ 116 05 <C 11 0∞
144: 0∞ 116 <C 16 0∞ (via chain step)
145: 0∞ 115 <A 17 0∞
146: 0∞ 114 <D 18 0∞
147: 0∞ 113 01 D> 18 0∞
155: 0∞ 113 09 D> 0∞ (via chain step)
156: 0∞ 113 010 C> 0∞
So, we are back in the same configuration except that there are 3 fewer 1s and 5 more 0s. This behavior is, in fact, independent of the exact values of the exponents. Let’s see by generalizing the exponents:
0∞ 1n+3 0m C> 0∞
0∞ 1n+3 0m <C 11 0∞ (in 1 step)
0∞ 1n+3 <C 1m+1 0∞ (in m steps, m+1 total)
0∞ 1n+2 <A 1m+2 0∞ (in 1 step, m+2 total)
0∞ 1n+1 <D 1m+3 0∞ (in 1 step, m+3 total)
0∞ 1n 01 D> 1m+3 0∞ (in 1 step, m+4 total)
0∞ 1n 0m+4 D> 0∞ (in m+3 steps, 2m+7 total)
0∞ 1n 0m+5 C> 0∞ (in 1 step, 2m+8 total)
So, we now have a general rule that 0∞ 1n+3 0m C> 0∞ → 0∞ 1n 0m+5 C> 0∞ in 2m+8 steps (as long as n, m ≥ 0). Rather than writing out this configuration completely each time, let’s define g(n, m) = 0∞ 1n 0m C> 0∞. Now we can restate our rule as:
g(n+3, m) → g(n, m+5) in 2m+8 steps
(Note that this rule only applies for n, m ≥ 0, rather than writing that out every time, I will simply use the convention that all rules apply for all variable ≥ 0. This is why I didn’t write this rule as g(n, m) → g(n-3, m+5))
I call this a rule step.
Repeated Application of Rule Steps
This rule is especially nice because you can apply it repeatedly. So for example, going back to step 138 where our TM configuration is g(16, 5) = 0∞ 116 05 C> 0∞ we can see the evaluation:
g(16, 5) → g(13, 10) → g(10, 15) → g(7, 20) → g(4, 25) → g(1, 30)
In fact, rather than manually applying this function multiple times, we can jump straight from the beginning to the end!
g(3k + r, m) → g(r, 5k + m)
In other words, applying our rule k times removes 3k from the first parameter (the 1s count) and adds 5k to the second parameter (the 0s count).
Computing steps
As a small aside, how many steps does this take? That is a little more grungy. Remember that g(a+3, b) → g(a, b+5) in 2b+8 steps, but as we repeatedly apply this rule the value of the second parameter (b) is changing! So, to compute the steps from g(3k + r, m) → g(r, 5k + m) we must compute this series:
sum(2b + 8
where b = 5j + m
for j in 0..k-1)
= sum(10j + 2m + 8
for j in 0..k-1)
= 10 * sum(j for j in 0..k-1) + (2m + 8) * k
= 10 * k * (k-1) / 2 + (2m + 8) * k
= 5k^2 + (2m + 3) k
Collatz-like Behavior
We have come a long way towards understanding the behavior of this TM, the remaining open question is what happens to g(n, m) when n < 3? For this we must go back to the tape representation. We will consider each case separately:
g(0, m) = 0∞ 10 0m C> 0∞ = 0∞ C> 0∞
0∞ C> 0∞
0∞ <C 11 0∞
<C 1∞ 0∞
This last step is a bit tongue-in-cheek, but effectively, at this point the TM runs forever to the left in state C trailing 1s. Since it remains in state C forever after, it has “quasihalted” at this point!
g(1, m) = 0∞ 11 0m C> 0∞
0∞ 11 0m C> 0∞
0∞ 11 0m <C 11 0∞ (in 1 step)
0∞ 11 <C 1m+1 0∞ (in m steps, m+1 total)
0∞ <A 1m+2 0∞ (in 1 step, m+2 total)
0∞ 11 B> 1m+2 0∞ (in 1 step, m+3 total)
0∞ 1m+3 B> 0∞ (in m+2 step, 2m+5 total)
0∞ 1m+4 C> 0∞ (in 1 step, 2m+6 total)
So, g(1, m) → g(m+4, 0) in 2m + 6 steps.
g(2, m) = 0∞ 12 0m C> 0∞
0∞ 12 0m C> 0∞
0∞ 12 0m <C 11 0∞ (in 1 step)
0∞ 12 <C 1m+1 0∞ (in m steps, m+1 total)
0∞ 11 <A 1m+2 0∞ (in 1 step, m+2 total)
0∞ <D 1m+3 0∞ (in 1 step, m+3 total)
0∞ C> 1m+3 0∞ (in 1 step, m+4 total)
0∞ <A 1m+3 0∞ (in 1 step, m+5 total)
0∞ 11 B> 1m+3 0∞ (in 1 step, m+6 total)
0∞ 1m+4 B> 0∞ (in m+3 step, 2m+9 total)
0∞ 1m+5 C> 0∞ (in 1 step, 2m+10 total)
So, g(2, m) → g(m+5, 0) in 2m + 10 steps.
Collatz-like Function
Putting all of these together we can see that once the TM get’s into any configuration like g(n, m), we can completely describe that TMs behavior by using the above rules! Collecting them all together we have:
g(3k, 0) → g(0, 5k) → Quasihalt
g(3k + 1, 0) → g(1, 5k) → g(5k + 4, 0)
g(3k + 2, 0) → g(2, 5k) → g(5k + 5, 0)
In other words, the behavior of this TM is equivalent to the behavior of this Collatz-like function of type 3 → 5 (using the language from Pascal Michel’s paper “Problems in Number Theory from Busy Beaver Competition”):
f(3k) undefined
f(3k + 1) = 5k + 4
f(3k + 2) = 5k + 5
Stated explicitly, if the TM reaches state g(n, 0) = 0∞ 1n C> 0∞, then it will quasihalt if and only if there exists a t such that ft(n) is undefined.
Difficulty of Deciding Quasihalting
In other words, the difficulty of the Quasihalting problem for this specific TM (but considering arbitrary initial tapes) is at least as hard as solving the above Collatz-like problem (whether or not iterating f starting from a specific value ever reaches the undefined value). Collatz-like problems are, in general, believed to be quite difficult to solve. Famously, Erdős said about the original Collatz conjecture: “Mathematics may not be ready for such problems.”
Collatz Orbit from Blank Tape
However, for the purposes of the Beeping Busy Beaver, we do not need to solve the halting problem for this machine for all input tapes, only for the blank tape! And that can, in fact, be directly computed. First of all, note that the TM reaches configuration g(2, 0) on step 2. From there we can calculate the iterations of the function f (the orbit of 2 via f):
2 → 5 → 10 → 19 → 34 → 59 → 100 → 169 → 284 → 475
→ 794 → 1325 → 2210 → 3685 → 6144 → Quasihalt
What makes this TM so successful in the BBB is not only that it simulates a Collatz-like function, but also that it happens to have found a surprisingly long orbit (14 iterations before hitting the undefined state)!
Chance of Long Orbit
The following is definitely hand-wavy, but: To put this orbit into perspective, if you chose random values n, then you’d expect for 1/3 of them, f(n) would be undefined (those divisible by 3). If we assume that the remainders of of the output of f after dividing by 3 are “uniformly distributed”, then the chance of ft(n) being defined would be (2/3)t. Specifically in this case, the chance of f14(n) being defined is (2/3)14 = 0.3%. So if feels like this TM got very “lucky” that it found such a long orbit: f14(2) = 6144!
Of course, there is a selection bias here. We are searching for the TMs that run a long time before quasihalting and thus are finding these “lucky” TMs out of a pile of “unlucky” ones.
Use For TM Simulation Acceleration
I find that modeling a TM by Collatz-like behavior gives me a personal feeling of insight into what it’s doing. But in addition to that value, our software also uses this behavior to significantly accelerate simulation of long-running TMs. Without it we would never be able to simulate TMs like the current BB(6, 2) champion which runs for >1036,534 steps!