S(2,4) = 3932964
We now know definitively that
\[\begin{array}{lcr} S(2,4) & = & 3\,932\,964 \\ \Sigma(2,4) & = & 2\,050 \\ \end{array}\]So, all 2-state, 4-symbol Turing machines either halt within the first 4 million steps or run forever. Both of these records are set by a single TM (1RB2LA1RA1RA_1LB1LA3RB1RZ) the champion that my dad and I found in 2005 that started my Busy Beaver journey.
Proof
The \(S(2,4)\) bound was proven by @mxdys using a subset of methods that were used to prove the \(S(5) = 47\,176\,870\) result. See Coq-BB5/BB24Theorem.v for the self-contained Coq proof. The proof uses only the following deciders:
- Translated Cycler (
loop1_decider) - Ngram CPS (
NGramCPS_decider_impl1,NGramCPS_decider_impl2,NGramCPS_LRU_decider) RepWL_ES_decider(a CTL method)
You can check the proof for yourself by:
- Cloning the Coq-BB5 repo
- Installing Coq version 8.18 or newer
- Running
coqc -Q . BusyCoq BB24Theorem.v
On my Mac laptop it compiles within 20 minutes:
time coqc -Q . BusyCoq BB24Theorem.v
...
Axioms:
functional_extensionality_dep
: forall (A : Type) (B : A -> Type) (f g : forall x : A, B x),
(forall x : A, f x = g x) -> f = g
coqc -Q . BusyCoq BB24Theorem.v 1170.85s user 2.78s system 99% cpu 19:37.42 total
There are a couple of small caveats to note about this proof:
- It depends on one assumption/axiom: functional extensionality. I don’t think this is very controversial it basically just defines what it means for two functions to be equal (that for all inputs they produce the same outputs) and is a very common axiom to use in many proofs.
- Technically, the way that
@mxdysdefined TMs in this library they do not actually have halting states, but instead undefined transitions. The idea is that the TM halts once it reaches an undefined transition. This is a very minor difference with the standard TM definition used by Rado for Busy Beavers, but completely equivalent. However, you will notice in the code that they refer to the BB value as 3932963 (one less than the official value) because this is the number of steps until you reach an undefined transition. - The Coq proof does not prove the \(\Sigma(2,4)\) value. Instead for that we depend upon the slightly less rigorous process of manually running all 2-state, 4-symbol TMs for \(S(2,4)\) steps and noting by inspection that the champion indeed leaves the most non-zero symbols on the tape.
These caveats apply to the previous BB(5) proof as well.
Deciders
The heart of this proof computation is a TNF enumeration of all 2-state, 4-symbol TMs each of which is run through a series of 21 decider parameterizations:
(
(loop1_decider 107 (1::2::4::8::16::32::64::128::256::512::nil))::
(NGramCPS_decider_impl2 1 1 400)::
(NGramCPS_decider_impl2 2 2 800)::
(NGramCPS_decider_impl2 3 3 400)::
(NGramCPS_decider_impl2 4 4 800)::
(loop1_decider 4100 (1::2::4::8::16::32::64::128::256::512::1024::2048::4096::nil))::
(RepWL_ES_decider 2 3 320 400)::
(NGramCPS_LRU_decider 2 2 1000)::
(NGramCPS_decider_impl1 2 2 2 3000)::
(NGramCPS_decider_impl1 2 3 3 1600)::
(NGramCPS_decider_impl1 4 2 2 600)::
(NGramCPS_decider_impl1 4 3 3 1600)::
(NGramCPS_decider_impl1 6 2 2 3200)::
(NGramCPS_decider_impl1 6 3 3 3200)::
(NGramCPS_decider_impl1 8 2 2 1600)::
(NGramCPS_decider_impl1 8 3 3 1600)::
(NGramCPS_LRU_decider 3 3 20000)::
(RepWL_ES_decider 4 2 320 2000)::
(RepWL_ES_decider 6 2 320 2000)::
(NGramCPS_decider_impl2 4 4 20000)::
(halt_decider 3932964)::
nil
)
These are run in order. I expect that the order here is meant to roughly correspond to the most “efficient” order. In other words, the decider parameterizations near the top presumably decide more TMs more quickly than the ones further down the list. However, I don’t know how optimal this order is or if a tweak to it would allow the proof to run more quickly.
The deciders used here fall into 3 broad groups as I mentioned earlier:
- Translated Cycle (
loop1_decider) - Ngram CPS (
NGramCPS_decider_impl1,NGramCPS_decider_impl2,NGramCPS_LRU_decider) - CTL (
RepWL_ES_decider)
A natural question to ask is how important are each of these deciders? For example, how many TMs are decided by each? Coq code does not make it easy to add instrumentation, however, I was able to extract a little bit of information. If you comment out all of the RepWL_ES_deciders, then it leaves 102 holdout TMs. So we can see that Translated Cycler + Ngram CPS is almost strong enough to solve BB(2,4), but not quite.
Regular TMs
One interesting result here is that all deciders used to prove the BB(2,4) result are “regular” deciders. In other words, every non-halting BB(2,4) TM can be proven infinite using CTL using Regular Expressions. This was not true for BB(5) where it was discovered that there were approximately 30 5-state, 2-symbol TMs which appear to be “irregular” (i.e. unable to be proven infinite via CTL using Regular Expressions) and at least some of them were proven irregular.
When paired with the result that we have found Crypids in BB(6,2), BB(3,3) and BB(2,5) we see that BB(5) has the surprisingly unique experience of being the only domain in which there are irregular TMs, but no Cryptids. In other words, that there are TMs which are “hard” to prove (requiring deciders more powerful than regular languages) but not too hard (requiring solving a Collatz-like problem). This was first noted by @mxdys on Discord where he posted the following image to demonstrate:
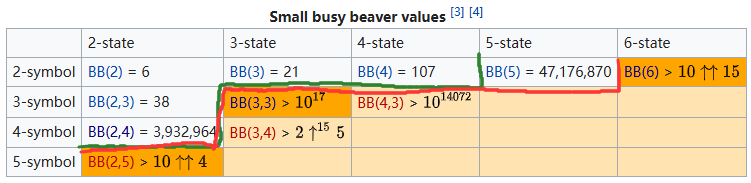
Here the green line bounds domains where all TMs are regular (CTLable) and the red line bounds all domains that don’t contain Cryptids. The only deviation is BB(5).
Is this mathematically meaningful? I think the answer is no, it’s basically a coincidence of the precise way that we define TMs for the Busy Beaver problem. If you were to use a slightly different definition of computation (TMs with semi-infinite tape, 4-tuple TMs, lambda calculus, etc.) I think you’d end up with a completely different result. But from a social point of view, it’s quite intriguing. We at http://bbchallenge.org ended up focusing our efforts on this unique BB(5) case which turned out to be solvable but did require a bit of uniquely challenging ingenuity.
History
Note: All Discord links are for the https://bbchallenge.org/ Discord server.
BB(2,4) was first informally decided through a collaboration between myself and @Iijil in 2023:
- On 10 Apr 2023,
@Iijilshared a list of 27 BB(2,4) holdout TMs (Discord). - The same day, I shared my list of 31 holdouts (Discord).
- There were only 2 TMs in both lists:
1RB3LA1LA1RA_2LB2RA---0RBand1RB3LA1LA2RA_2LB3RA---0RB. In other words, only 2 TMs that neither of us had proven infinite yet. @Iijilran theirMITMWFARdecider to higher parameters (14 non-dead transitions) and was able to decide the last 2 TMs (Discord).- Last week, Andrew Ducharme and my dad reproduced this result (Discord).
- On 22 Aug 2024,
@mxdysannounced that they had successfully compiled the Coq proof of BB(2,4) (Discord).