I was worried my WikiTree Network Definition post was going to put everyone to sleep, but in contrast, you all just asked me for even more nitty-gritty details! I love it! So I’ve decided to delay my next article in order to add a follow-up Q&A post. Specifically:

  • Eva asked how we handle more complicated examples, such as people with multiple marriages.
  • Bernard asked how distance measurements relate between these 3 network models.

These are great questions and I think get to the heart of some of the (perhaps arbitrary) decisions that I (and the WikiTree connection finder folks) have made in the precise details of how these models are defined.

These two questions are actually intertwined in the sense that I can answer Bernard’s question (about relating distance measurements) concisely if a network doesn’t have these complicated scenarios. But it becomes more complicated once we consider different corner cases.

Complicated Example

There are several cases that I know of that lead to some complication between networks:

  1. A person with multiple marriages
  2. Unmarried people having children together
  3. People only one parent listed
  4. People with no parents listed

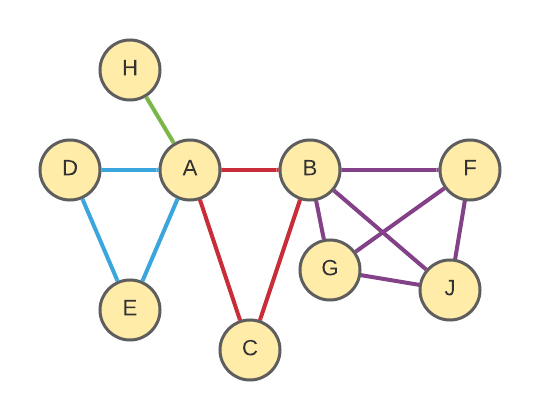
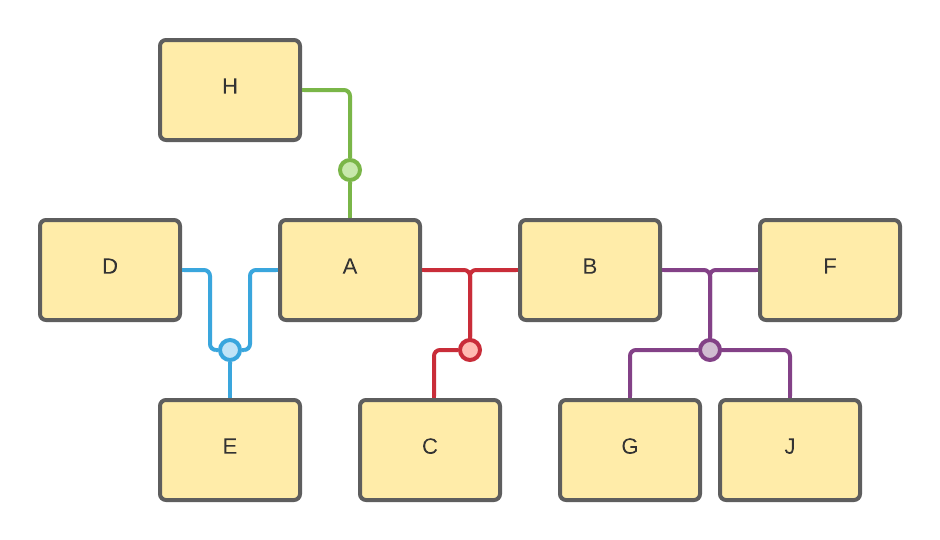
And here’s a tree with all of these wrapped up together: Complex Tree

Let me explain this one to make sure my notation is clear!

  • A married B and they had child C
  • A did not marry D, but they had a child E together
  • B also married F and they had children G & J
  • We only know one parent of A: H
  • We don’t know either parents of B

Person Network

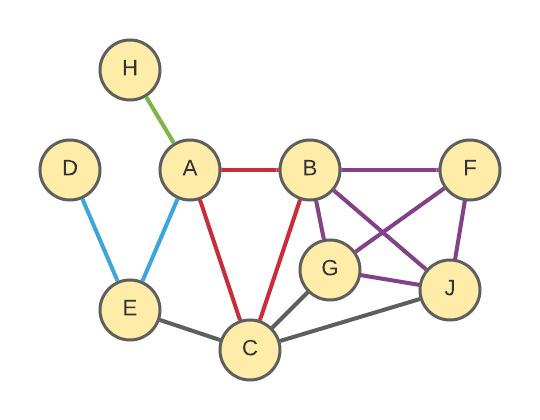
Complex Person Network

Notable details here:

  • A & D are not connected directly because they never married.
  • C is connected directly to E, G & J because they are (half-)siblings (they share a parent). Since those connections are not part of any single “Nuclear Family unit”, I color them black.
  • E & G (step-siblings) are not directly connected because they do not share either parent.

I made these choices in order to emulate the WikiTree Connection Finder. If these details differ from how the Connection Finder actually works, let me know and I’ll update my code :)

Bipartite Network

Complex Bipartite Network

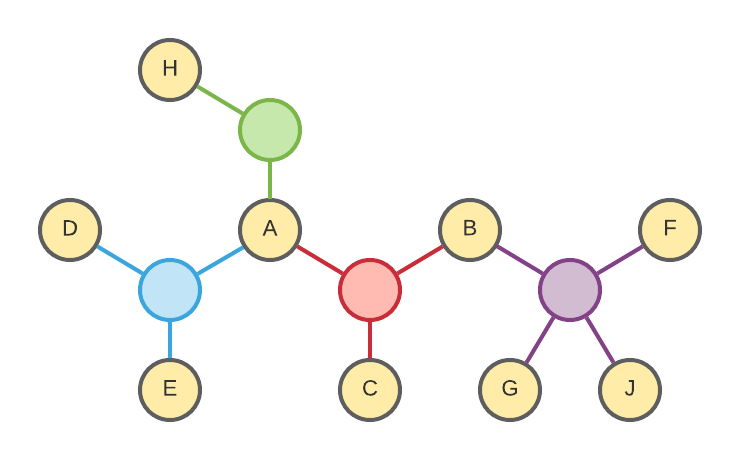
Notable details here:

  • We do not distinguish between a married couple and unmarried co-parents. In other words the DAE subnetwork here is identical to the ABC subnetwork.
  • Half-siblings more distant than full siblings, you must travel up through their shared parent and back down.

Family Network

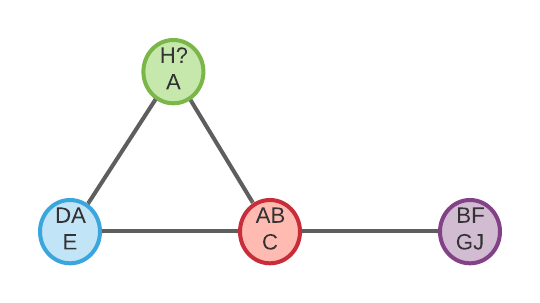
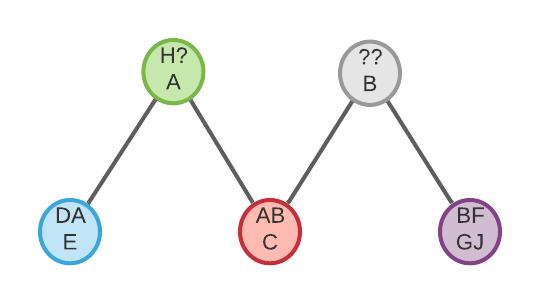
Complex Family Network

Notable details here:

  • The same as in the Bipartite Network, we do not distinguish between a married couple and unmarried co-parents.
  • There is no direct connection between Family DAE and ABC (or between ABC & BFGJ) instead you have to travel through the parent node (H?A) to connect them. I could have chosen to connect these nodes directly (they share a person in common). In fact my original Family Network did connect re-marriage families together, however that led to cliques re-appearing for people who married many times. As an extreme example: Brigham Young ended up causing a 56-node clique (with his 55 wives and one birth family) which had 1540 edges! The whole point of creating the Family Network was to avoid these sorts of giant cliques, so I changed my definition so that there would only be edges between the childhood family and each adult family (not between re-marriages).
  • I’ve added a virtual parent node for B (Grey node: ??B). Without this node, ABC and BFGJ would be completely disconnected which totally changes the connectivity of the network. So instead we just imagine that we had a stub profile for B’s parents (with no names or siblings, etc). [Side note: Adding these virtual parent nodes leads to a 2% node increases and 4% edge increase.]

Distances

OK, I think that answers Eva’s question, we are now almost ready to target Bernard’s. What is the relationship between shortest path distances between two people in these various networks?

Bipartite Network Projection

There is one tool that will be very helpful in comparing the distance metrics on these 3 networks: the Bipartite Network Projection. Well that’s quite a pile of jargon, what is it? Well it is a way to turn a bipartite network into a normal network. You can project a bipartite network onto either of its node types. Let me define the projection of our Bipartite Network onto its Person nodes: The new network will have all the Person nodes from the Bipartite Network and two Person nodes will be connected directly if they were both adjacent to the same Family node. In other words, we connect all members of a family to each other. Let’s call this the “Projected Person Network”. For our example it looks like:

Complex Projected Person Network

Notably, this looks almost identical to our Person Network with 2 differences:

  1. Half-siblings are no longer connected.
  2. Unmarried co-parents (D & A) are now connected.

This was the projection onto the Person nodes, but we can also project the Bipartite Network onto the Family nodes by the analogous method: All Family nodes from the Bipartite Network become nodes in our new network, they are connected if they share a Person in common. We’ll call this one the “Projected Family Network”:

Complex Projected Family Network

Notably, this looks very similar to our Family Network with 2 differences:

  1. Re-marriages are now connected (DAE to ABC and ABC to BFGJ).
  2. We no longer need the virtual (??B) node to keep the network connected.

Distance Properties of Projection

Alright, why have I just introduced you to yet 2 more networks and this whole Network Projection concept? Well comparing distances on a bipartite network to its projections is super-simple: The distance between two points on a projection is exactly half of the distance on the original bipartite network! You can see this because every edge in the projected network represents two edges in the original bipartite network (for example, the edge A->B in the Projected Person Network above represents the edges A->Red->B in the original Bipartite Network).

So, if our original Person Network was identical to this new Projected Person Network, then we would know that distances in the Bipartite Network would be exactly twice the distances in the Person Network (the Connection Finder distances). Unfortunately, they are not the same. WikiTree Connection Finder developers decided to make half-siblings directly connected and unmarried co-parents unconnected and so the distance measurements between these two networks are non-trivial to compare. In general, I expect that distances in the Person Network graph will be roughly half as much as in the Bipartite Network, but not always exactly.

Likewise, if my Family Network was identical to this new Projected Family Network, then we would know that distances in the Bipartite Network would be exactly twice the distances in the Family Network. In this case, I am the one to blame. As mentioned above, I have avoided connecting re-marriages to each other to try and avoid cliques in the network (and because of that had to introduce the virtual parent nodes). So once again, in general, I expect that distances in the Family Network graph will be roughly half as much as in the Bipartite Network and thus roughly equal to distances in the Person Network, but not always exactly.

(Comments and discussion at WikiTree G2G)

This article is part of a series on the WikiTree Network:

  1. WikiTree and Network Theory

  2. The WikiTree Network Definition

  3. WikiTree Network Corner Cases

  4. WikiTree Network Degree Distribution